Square number

Template:Short description Template:More footnotes In mathematics, a square number or perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 9 is a square number, since it can be written as Template:Math.

The usual notation for the square of a number Template:Mvar is not the product Template:Math, but the equivalent exponentiation Template:Math, usually pronounced as "Template:Mvar squared". The name square number comes from the name of the shape. The unit of area is defined as the area of a unit square (Template:Math). Hence, a square with side length Template:Mvar has area Template:Math.

Square numbers are non-negative. Another way of saying that a (non-negative) integer is a square number is that its square root is again an integer. For example, Template:Sqrt = 3, so 9 is a square number.

A positive integer that has no perfect square divisors except 1 is called square-free.

For a non-negative integer Template:Mvar, the Template:Mvarth square number is Template:Math, with Template:Math being the zeroth one. The concept of square can be extended to some other number systems. If rational numbers are included, then a square is the ratio of two square integers, and, conversely, the ratio of two square integers is a square, e.g., $\textstyle {\frac {4}{9}}=\left({\frac {2}{3}}\right)^{2}$.

Starting with 1, there are Template:Math square numbers up to and including Template:Mvar, where the expression Template:Math represents the floor of the number Template:Mvar.

Examples

The squares Template:OEIS smaller than 60² = 3600 are:

0² = 0

1² = 1

2² = 4

3² = 9

4² = 16

5² = 25

6² = 36

7² = 49

8² = 64

9² = 81

10² = 100

11² = 121

12² = 144

13² = 169

14² = 196

15² = 225

16² = 256

17² = 289

18² = 324

19² = 361

20² = 400

21² = 441

22² = 484

23² = 529

24² = 576

25² = 625

26² = 676

27² = 729

28² = 784

29² = 841

30² = 900

31² = 961

32² = 1024

33² = 1089

34² = 1156

35² = 1225

36² = 1296

37² = 1369

38² = 1444

39² = 1521

40² = 1600

41² = 1681

42² = 1764

43² = 1849

44² = 1936

45² = 2025

46² = 2116

47² = 2209

48² = 2304

49² = 2401

50² = 2500

51² = 2601

52² = 2704

53² = 2809

54² = 2916

55² = 3025

56² = 3136

57² = 3249

58² = 3364

59² = 3481

The difference between any perfect square and its predecessor is given by the identity Template:Math. Equivalently, it is possible to count up square numbers by adding together the last square, the last square's root, and the current root, that is, Template:Math.

Properties

The number Template:Mvar is a square number if and only if one can arrange Template:Mvar points in a square:

Template:Bigmath
Template:Bigmath
Template:Bigmath
Template:Bigmath
Template:Bigmath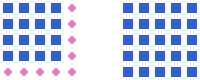

The expression for the Template:Mvarth square number is Template:Math. This is also equal to the sum of the first Template:Mvar odd numbers as can be seen in the above pictures, where a square results from the previous one by adding an odd number of points (shown in magenta). The formula follows:

$n^{2}=\sum _{k=1}^{n}(2k-1).$

For example, Template:Math.

There are several recursive methods for computing square numbers. For example, the Template:Mvarth square number can be computed from the previous square by Template:Math. Alternatively, the Template:Mvarth square number can be calculated from the previous two by doubling the Template:Mathth square, subtracting the Template:Mathth square number, and adding 2, because Template:Math. For example,

Template:Math.

One number less than a square (m - 1) is always the product of Template:Sqrt - 1 and Template:Sqrt + 1 (e.g. 8 × 6 equals 48, while 7Template:Sup equals 49). Thus, 3 is the only prime number one less than a square.

A square number is also the sum of two consecutive triangular numbers. The sum of two consecutive square numbers is a centered square number. Every odd square is also a centered octagonal number.

Another property of a square number is that (except 0) it has an odd number of positive divisors, while other natural numbers have an even number of positive divisors. An integer root is the only divisor that pairs up with itself to yield the square number, while other divisors come in pairs.

Lagrange's four-square theorem states that any positive integer can be written as the sum of four or fewer perfect squares. Three squares are not sufficient for numbers of the form Template:Math. A positive integer can be represented as a sum of two squares precisely if its prime factorization contains no odd powers of primes of the form Template:Math. This is generalized by Waring's problem.

In base 10, a square number can end only with digits 0, 1,  4,  5, 6 or  9, as follows:

• if the last digit of a number is 0, its square ends in 0 (in fact, the last two digits must be 00);
• if the last digit of a number is 1 or 9, its square ends in 1;
• if the last digit of a number is 2 or 8, its square ends in 4;
• if the last digit of a number is 3 or 7, its square ends in 9;
• if the last digit of a number is 4 or 6, its square ends in 6; and
• if the last digit of a number is 5, its square ends in 5 (in fact, the last two digits must be 25).

In base 12, a square number can end only with square digits (like in base 12, a prime number can end only with prime digits or 1), i.e. 0, 1, 4 or 9, as follows:

• if a number is divisible both by 2 and by 3 (i.e. divisible by 6), its square ends in 0;
• if a number is divisible neither by 2 nor by 3, its square ends in 1;
• if a number is divisible by 2, but not by 3, its square ends in 4; and
• if a number is not divisible by 2, but by 3, its square ends in 9.

Similar rules can be given for other bases, or for earlier digits (the tens instead of the units digit, for example).Template:Cn All such rules can be proved by checking a fixed number of cases and using modular arithmetic.

In general, if a prime Template:Mvar divides a square number Template:Mvar then the square of Template:Mvar must also divide Template:Mvar; if Template:Mvar fails to divide Template:Math, then Template:Mvar is definitely not square. Repeating the divisions of the previous sentence, one concludes that every prime must divide a given perfect square an even number of times (including possibly 0 times). Thus, the number Template:Mvar is a square number if and only if, in its canonical representation, all exponents are even.

Squarity testing can be used as alternative way in factorization of large numbers. Instead of testing for divisibility, test for squarity: for given Template:Mvar and some number Template:Mvar, if Template:Math is the square of an integer Template:Mvar then Template:Math divides Template:Mvar. (This is an application of the factorization of a difference of two squares.) For example, Template:Math is the square of 3, so consequently Template:Math divides 9991. This test is deterministic for odd divisors in the range from Template:Math to Template:Math where Template:Mvar covers some range of natural numbers Template:Math.

A square number cannot be a perfect number.

The sum of the n first square numbers is

$\sum _{n=0}^{N}n^{2}=0^{2}+1^{2}+2^{2}+3^{2}+4^{2}+\cdots +N^{2}={\frac {N(N+1)(2N+1)}{6}}.$

The first values of these sums, the square pyramidal numbers, are: Template:OEIS

0, 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525, 6201...

The sum of the first odd integers, beginning with one, is a perfect square: 1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 + 7, etc.

The sum of the n first cubes is the square of the sum of the n first positive integers; this is Nicomachus's theorem.

All fourth powers, sixth powers, eighth powers and so on are perfect squares.

Special cases

• If the number is of the form Template:Math where Template:Math represents the preceding digits, its square is Template:Math where Template:Math and represents digits before 25. For example, the square of 65 can be calculated by Template:Math which makes the square equal to 4225.
• If the number is of the form Template:Math where Template:Math represents the preceding digits, its square is Template:Math where Template:Math. For example, the square of 70 is 4900.
• If the number has two digits and is of the form Template:Math where Template:Math represents the units digit, its square is Template:Math where Template:Math and Template:Math. Example: To calculate the square of 57, 25 + 7 = 32 and 7² = 49, which means 57² = 3249.
• If the number ends in 5, its square will end in 5; similarly for ending in 25, 625, 0625, 90625, ... 8212890625, etc. If the number ends in 6, its square will end in 6, similarly for ending in 76, 376, 9376, 09376, ... 1787109376. For example, the square of 55376 is 3066501376, both ending in 376. (The numbers 5, 6, 25, 76, etc. are called automorphic numbers. They are sequence A003226 in the OEIS.)

Odd and even square numbers

Squares of even numbers are even (and in fact divisible by 4), since Template:Math.

Squares of odd numbers are odd, since Template:Math.

It follows that square roots of even square numbers are even, and square roots of odd square numbers are odd.

As all even square numbers are divisible by 4, the even numbers of the form Template:Math are not square numbers.

As all odd square numbers are of the form Template:Math, the odd numbers of the form Template:Math are not square numbers.

Squares of odd numbers are of the form Template:Math, since Template:Math and Template:Math is an even number.

Every odd perfect square is a centered octagonal number. The difference between any two odd perfect squares is a multiple of 8. The difference between 1 and any higher odd perfect square always is eight times a triangular number, while the difference between 9 and any higher odd perfect square is eight times a triangular number minus eight. Since all triangular numbers have an odd factor, but no two values of Template:Math differ by an amount containing an odd factor, the only perfect square of the form Template:Math is 1, and the only perfect square of the form Template:Math is 9.

See also

• Brahmagupta–Fibonacci identity
• Cubic number
• Euler's four-square identity
• Fermat's theorem on sums of two squares
• Integer square root
• Methods of computing square roots
• Polygonal number
• Power of two
• Pythagorean triple
• Quadratic residue
• Quadratic function
• Square (algebra)#Related identities
• Square triangular number
• Wallis sieve

Further reading

• Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 30–32, 1996. Template:Isbn
• Kiran Parulekar. Amazing Properties of Squares and Their Calculations. Kiran Anil Parulekar, 2012 https://books.google.com/books?id=njEtt7rfexEC&source=gbs_navlinks_s

External links

• Learn Square Numbers. Practice square numbers up to 144 with this children's multiplication game
• Dario Alpern, Sum of squares. A Java applet to decompose a natural number into a sum of up to four squares.
• Fibonacci and Square Numbers at Convergence