Polygonal number

In mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots are thought of as alphas (units). These are one type of 2-dimensional figurate numbers.

Definition and examples

The number 10 for example, can be arranged as a triangle (see triangular number):

But 10 cannot be arranged as a square. The number 9, on the other hand, can be (see square number):

Some numbers, like 36, can be arranged both as a square and as a triangle (see square triangular number):

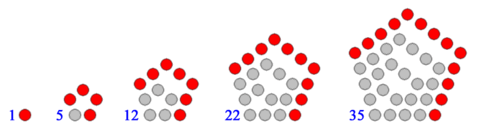
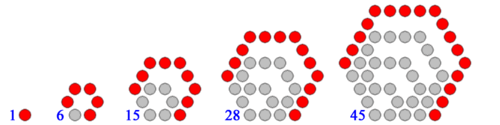
By convention, 1 is the first polygonal number for any number of sides. The rule for enlarging the polygon to the next size is to extend two adjacent arms by one point and to then add the required extra sides between those points. In the following diagrams, each extra layer is shown as in red.

Triangular numbers

Square numbers

Polygons with higher numbers of sides, such as pentagons and hexagons, can also be constructed according to this rule, although the dots will no longer form a perfectly regular lattice like above.

Pentagonal numbers

Hexagonal numbers

Formula

If Template:Mvar is the number of sides in a polygon, the formula for the Template:Mvarth Template:Mvar-gonal number Template:Math is

$P(s,n)={\frac {n^{2}(s-2)-n(s-4)}{2}}$

or

$P(s,n)=(s-2){\frac {n(n-1)}{2}}+n$

The Template:Mvarth Template:Mvar-gonal number is also related to the triangular numbers Template:Math as follows:

$P(s,n)=(s-2)T_{n-1}+n=(s-3)T_{n-1}+T_{n}\,.$

Thus:

${\begin{aligned}P(s,n+1)-P(s,n)&=(s-2)n+1\,,\\P(s+1,n)-P(s,n)&=T_{n-1}={\frac {n(n-1)}{2}}\,.\end{aligned}}$

For a given Template:Mvar-gonal number Template:Math, one can find Template:Mvar by

$n={\frac {{\sqrt {8(s-2)x+{(s-4)}^{2}}}+(s-4)}{2(s-2)}}$

and one can find Template:Mvar by

$s=2+{\frac {2}{n}}\cdot {\frac {x-n}{n-1}}$.

Every hexagonal number is also a triangular number

Applying the formula above:

$P(s,n)=(s-2)T_{n-1}+n$

to the case of 6 sides gives:

$P(6,n)=4T_{n-1}+n$

but since:

$T_{n-1}={\frac {n(n-1)}{2}}$

it follows that:

$P(6,n)={\frac {4n(n-1)}{2}}+n={\frac {2n(2n-1)}{2}}=T_{2n-1}$

This shows that the Template:Mvarth hexagonal number Template:Math is also the Template:Mathth triangular number Template:Math. We can find every hexagonal number by simply taking the odd-numbered triangular numbers:

1, 3, 6, 10,15, 21, 28, 36, 45, 55, 66, ...

Table of values

The first 6 values in the column "sum of reciprocals", for triangular to octagonal numbers, come from a published solution to the general problem, which also gives a general formula for any number of sides, in terms of the digamma function.

Template:Mvar	Name	Formula	Template:Mvar										Sum of reciprocals	OEIS number
			1	2	3	4	5	6	7	8	9	10
3	Triangular	Template:Math	1	3	6	10	15	21	28	36	45	55	2	Template:OEIS link
4	Square	Template:Math	1	4	9	16	25	36	49	64	81	100	Template:Sfrac	Template:OEIS link
5	Pentagonal	Template:Math	1	5	12	22	35	51	70	92	117	145	Template:Math	Template:OEIS link
6	Hexagonal	Template:Math	1	6	15	28	45	66	91	120	153	190	Template:Math	Template:OEIS link
7	Heptagonal	Template:Math	1	7	18	34	55	81	112	148	189	235	${\begin{matrix}{\tfrac {2}{3}}\ln 5\\+{\tfrac {{1}+{\sqrt {5}}}{3}}\ln {\tfrac {\sqrt {10-2{\sqrt {5}}}}{2}}\\+{\tfrac {{1}-{\sqrt {5}}}{3}}\ln {\tfrac {\sqrt {10+2{\sqrt {5}}}}{2}}\\+{\tfrac {\pi {\sqrt {25-10{\sqrt {5}}}}}{15}}\end{matrix}}$	Template:OEIS link
8	Octagonal	Template:Math	1	8	21	40	65	96	133	176	225	280	Template:Math	Template:OEIS link
9	Nonagonal	Template:Math	1	9	24	46	75	111	154	204	261	325		Template:OEIS link
10	Decagonal	Template:Math	1	10	27	52	85	126	175	232	297	370	Template:Math	Template:OEIS link
11	Hendecagonal	Template:Math	1	11	30	58	95	141	196	260	333	415		Template:OEIS link
12	Dodecagonal	Template:Math	1	12	33	64	105	156	217	288	369	460		Template:OEIS link
13	Tridecagonal	Template:Math	1	13	36	70	115	171	238	316	405	505		Template:OEIS link
14	Tetradecagonal	Template:Math	1	14	39	76	125	186	259	344	441	550	Template:Math	Template:OEIS link
15	Pentadecagonal	Template:Math	1	15	42	82	135	201	280	372	477	595		Template:OEIS link
16	Hexadecagonal	Template:Math	1	16	45	88	145	216	301	400	513	640		Template:OEIS link
17	Heptadecagonal	Template:Math	1	17	48	94	155	231	322	428	549	685		Template:OEIS link
18	Octadecagonal	Template:Math	1	18	51	100	165	246	343	456	585	730	Template:Math Template:Math	Template:OEIS link
19	Enneadecagonal	Template:Math	1	19	54	106	175	261	364	484	621	775		Template:OEIS link
20	Icosagonal	Template:Math	1	20	57	112	185	276	385	512	657	820		Template:OEIS link
21	Icosihenagonal	Template:Math	1	21	60	118	195	291	406	540	693	865		Template:OEIS link
22	Icosidigonal	Template:Math	1	22	63	124	205	306	427	568	729	910		Template:OEIS link
23	Icositrigonal	Template:Math	1	23	66	130	215	321	448	596	765	955		Template:OEIS link
24	Icositetragonal	Template:Math	1	24	69	136	225	336	469	624	801	1000		Template:OEIS link
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
10000	Myriagonal	Template:Math	1	10000	29997	59992	99985	149976	209965	279952	359937	449920		Template:OEIS link

The On-Line Encyclopedia of Integer Sequences eschews terms using Greek prefixes (e.g., "octagonal") in favor of terms using numerals (i.e., "8-gonal").

A property of this table can be expressed by the following identity (see Template:OEIS link):

$2\,P(s,n)=P(s+k,n)+P(s-k,n),$

with

$k=0,1,2,3,...,s-3.$

Combinations

Some numbers, such as 36 which is both square and triangular, fall into two polygonal sets. The problem of determining, given two such sets, all numbers that belong to both can be solved by reducing the problem to Pell's equation. The simplest example of this is the sequence of square triangular numbers.

The following table summarizes the set of Template:Mvar-gonal Template:Mvar-gonal numbers for small values of Template:Mvar and Template:Mvar.

Template:Mvar	Template:Mvar	Sequence	OEIS number
4	3	1, 36, 1225, 41616, 1413721, 48024900, 1631432881, 55420693056, 1882672131025, 63955431761796, 2172602007770041, 73804512832419600, 2507180834294496361, 85170343853180456676, 2893284510173841030625, 98286503002057414584576, 3338847817559778254844961, ...	Template:OEIS link
5	3	1, 210, 40755, 7906276, 1533776805, 297544793910, 57722156241751, 11197800766105800, 2172315626468283465, …	Template:OEIS link
5	4	1, 9801, 94109401, 903638458801, 8676736387298001, 83314021887196947001, 799981229484128697805801, ...	Template:OEIS link
6	3	All hexagonal numbers are also triangular.	Template:OEIS link
6	5	1, 40755, 1533776805, …	Template:OEIS link
7	3	1, 55, 121771, 5720653, 12625478965, 593128762435, 1309034909945503, 61496776341083161, 135723357520344181225, 6376108764003055554511, 14072069153115290487843091, …	Template:OEIS link
7	4	1, 81, 5929, 2307361, 168662169, 12328771225, 4797839017609, 350709705290025, 25635978392186449, 9976444135331412025, …	Template:OEIS link
7	5	1, 4347, 16701685, 64167869935, …	Template:OEIS link
7	6	1, 121771, 12625478965, …	Template:OEIS link
8	3	1, 21, 11781, 203841, …	Template:OEIS link
8	4	1, 225, 43681, 8473921, 1643897025, 318907548961, 61866420601441, 12001766689130625, 2328280871270739841, 451674487259834398561, 87622522247536602581025, 16998317641534841066320321, …	Template:OEIS link
8	5	1, 176, 1575425, 234631320, …	Template:OEIS link
8	6	1, 11781, 113123361, …	Template:OEIS link
8	7	1, 297045, 69010153345, …	Template:OEIS link
9	3	1, 325, 82621, 20985481, …	Template:OEIS link
9	4	1, 9, 1089, 8281, 978121, 7436529, 878351769, 6677994961, 788758910641, 5996832038649, 708304623404049, 5385148492712041, 636056763057925561, ...	Template:OEIS link
9	5	1, 651, 180868051, …	Template:OEIS link
9	6	1, 325, 5330229625, …	Template:OEIS link
9	7	1, 26884, 542041975, …	Template:OEIS link
9	8	1, 631125, 286703855361, …	Template:OEIS link

In some cases, such as Template:Math and Template:Math, there are no numbers in both sets other than 1.

The problem of finding numbers that belong to three polygonal sets is more difficult. A computer search for pentagonal square triangular numbers has yielded only the trivial value of 1, though a proof that there are no other such numbers has yet to be found.

The number 1225 is hecatonicositetragonal (Template:Math), hexacontagonal (Template:Math), icosienneagonal (Template:Math), hexagonal, square, and triangular.

The only polygonal set that is contained entirely in another polygonal set is the set of hexagonal numbers, which is contained in the set of triangular numbers.Template:Citation needed

See also

• Polyhedral number
• Fermat polygonal number theorem

References

• The Penguin Dictionary of Curious and Interesting Numbers, David Wells (Penguin Books, 1997) [[[:Template:Isbn]]].
• Polygonal numbers at PlanetMath
• Template:MathWorld
• Template:Cite book

External links

• Template:Springer
• Polygonal Numbers: Every s-polygonal number between 1 and 1000 clickable for 2<=s<=337
• Template:Youtube
• Polygonal Number Counting Function: http://www.mathisfunforum.com/viewtopic.php?id=17853