Trivialism

From testwiki
Jump to navigation Jump to search
Trivialism in symbolic logic; Read as "given any proposition, it is a true proposition."

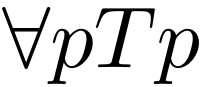
Trivialism (Template:Etymology) is the logical theory that all statements (also known as propositions) are true and that all contradictions of the form "p and not p" (e.g. the ball is red and not red) are true. In accordance with this, a trivialist is a person who believes everything is true.[1][2]

In classical logic, trivialism is in direct violation of Aristotle's law of noncontradiction. In philosophy, trivialism is considered by some to be the complete opposite of skepticism. Paraconsistent logics may use "the law of non-triviality" to abstain from trivialism in logical practices that involve true contradictions.

Theoretical arguments and anecdotes have been offered for trivialism to contrast it with theories such as modal realism, dialetheism and paraconsistent logics.

Overview

Etymology

Trivialism, as a term, is derived from the Latin word trivialis, meaning something that can be found everywhere. From this, "trivial" was used to suggest something was introductory or simple. In logic, from this meaning, a "trivial" theory is something regarded as defective in the face of a complex phenomenon that needs to be completely represented. Thus, literally, the trivialist theory is something expressed in the simplest possible way.[3]

Theory

In symbolic logic, trivialism may be expressed as the following:[4]

Template:Block indent

The above would be read as "given any proposition, it is a true proposition" through universal quantification (∀).

A claim of trivialism may always apply its fundamental truth, otherwise known as a truth predicate:

Template:Block indent

The above would be read as a "proposition if and only if a true proposition", meaning that all propositions are believed to be inherently proven as true. Without consistent use of this concept, a claim of advocating trivialism may not be seen as genuine and complete trivialism; as to claim a proposition is true but deny it as probably true may be considered inconsistent with the assumed theory.[4]

Taxonomy of trivialisms

Luis Estrada-González in "Models of Possiblism and Trivialism" lists four types of trivialism through the concept of possible worlds, with a "world" being a possibility and "the actual world" being reality. It is theorized a trivialist simply designates a value to all propositions in equivalence to seeing all propositions and their negations as true. This taxonomy is used to demonstrate the different strengths and plausibility of trivialism in this context:

  • (T0) Minimal trivialism: At some world, all propositions have a designated value.
  • (T1) Pluralist trivialism: In some worlds, all propositions have a designated value.
  • (T2) Actualist trivialism: In the actual world, all propositions have a designated value.
  • (T3) Absolute trivialism: In all worlds, all propositions have a designated value.[3]

Arguments against trivialism

The consensus among the majority of philosophers is descriptively a denial of trivialism, termed as non-trivialism or anti-trivialism.[3] This is due to it being unable to produce a sound argument through the principle of explosion and it being considered an absurdity (reductio ad absurdum).[2][4]

Aristotle

Aristotle's law of noncontradiction and other arguments are considered to be against trivialism. Luis Estrada-González in "Models of Possiblism and Trivialism" has interpreted Aristotle's Metaphysics Book IV as such: "A family of arguments between 1008a26 and 1007b12 of the form 'If trivialism is right, then X is the case, but if X is the case then all things are one. But it is impossible that all things are one, so trivialism is impossible.' ... these Aristotelian considerations are the seeds of virtually all subsequent suspicions against trivialism: Trivialism has to be rejected because it identifies what should not be identified, and is undesirable from a logical point of view because it identifies what is not identical, namely, truth and falsehood."[3]

Priest

Graham Priest considers trivialism untenable: "a substantial case can be made for [dialetheism]; belief in [trivialism], though, would appear to be grounds for certifiable insanity".[5]

He formulated the "law of non-triviality" as a replacement for the law of non-contradiction in paraconsistent logic and dialetheism.[6]

Arguments for trivialism

There are theoretical arguments for trivialism argued from the position of a devil's advocate:

Argument from possibilism

Paul Kabay has argued for trivialism in "On the Plenitude of Truth" from the following:

Template:Quote

Above, possibilism (modal realism; related to possible worlds) is the barely accepted theory that every proposition is possible. With this assumed to be true, trivialism can be assumed to be true as well according to Kabay.

Paradoxes

The liar's paradox, Curry's paradox, and the principle of explosion all can be asserted as valid and not required to be resolved and used to defend trivialism.[2][4]

Philosophical implications

Comparison to skepticism

In Paul Kabay's comparison of trivialism to schools of philosophical skepticism (in "On the Plenitude of Truth")—such as Pyrrhonism—who seek to attain a form of ataraxia, or state of imperturbability; it is purported the figurative trivialist inherently attains this state. This is claimed to be justified by the figurative trivialist seeing every state of affairs being true, even in a state of anxiety. Once universally accepted as true, the trivialist is free from any further anxieties regarding whether any state of affairs is true.

Kabay compares the Pyrrhonian skeptic to the figurative trivialist and claims that as the skeptic reportedly attains a state of imperturbability through a suspension of belief, the trivialist may attain such a state through an abundance of belief.

In this case—and according to independent claims by Graham Priest—trivialism is considered the complete opposite of skepticism.[2][4][7] However, insofar as the trivialist affirms all states of affairs as universally true, the Pyrrhonist neither affirms nor denies the truth (or falsity) of such affairs.[8]

Impossibility of action

It is asserted by both Priest and Kabay that it is impossible for a trivialist to truly choose and thus act. Priest argues this by the following in Doubt Truth to Be a Liar: "One cannot intend to act in such a way as to bring about some state of affairs, s, if one believes s already to hold. Conversely, if one acts with the purpose of bringing s about, one cannot believe that s already obtains."[6][9] Ironically, due to their suspension of determination upon striking equipollence between claims, the Pyrrhonist has also remained subject to apraxia charges.[10][11][12]

Advocates

Paul Kabay, an Australian philosopher, in his book A Defense of Trivialism has argued that various philosophers in history have held views resembling trivialism, although he stops short of calling them trivialists. He mentions various pre-Socratic Greek philosophers as philosophers holding views resembling trivialism. He mentions that Aristotle in his book Metaphysics appears to suggest that Heraclitus and Anaxagoras advocated trivialism. He quotes Anaxagoras as saying that all things are one. Kabay also suggests Heraclitus' ideas are similar to trivialism because Heraclitus believed in a union of opposites, shown in such quotes as "the way up and down is the same".[13] Kabay also mentions a fifteen century Roman Catholic cardinal Nicholas of Cusa, stating that what Cusa wrote in De Docta Ignorantia is interpreted as stating that God contained every fact, which Kabay argues would result in trivialism, but Kabay admits that mainstream Cusa scholars would not agree with interpreting Cusa as a trivialist.[14] Kabay also mentions Spinoza as a philosopher whose views resemble trivialism. Kabay argues Spinoza was a trivialist because Spinoza believed everything was made of one substance which had infinite attributes.[15] Kabay also mentions Hegel as a philosophers whose views resemble trivialism, quoting Hegel as stating in The Science of Logic "everything is inherently contradictory."[16]

Azzouni

Jody Azzouni is a purported advocate of trivialism in his article The Strengthened Liar by claiming that natural language is trivial and inconsistent through the existence of the liar paradox ("This sentence is false"), and claiming that natural language has developed without central direction. It is heavily implied by Azzouni that every sentence in any natural language is true.[17][18][19]

Anaxagoras

The Greek philosopher Anaxagoras is suggested as a possible trivialist by Graham Priest in his 2005 book Doubt Truth to Be a Liar. Priest writes, "He held that, at least at one time, everything was all mixed up so that no predicate applied to any one thing more than a contrary predicate."[6]

Anti-trivialism

Absolute anti-trivialism (or maximal logical nihilism) in symbolic logic; Read as "given any proposition, it is neither a true or false proposition."

Luis Estrada-González in "Models of Possiblism and Trivialism" lists eight types of anti-trivialism (or non-trivialism) through the use of possible worlds:

(AT0) Actualist minimal anti-trivialism: In the actual world, some propositions do not have a value of true or false.
(AT1) Actualist absolute anti-trivialism: In the actual world, all propositions do not have a value of true or false.
(AT2) Minimal anti-trivialism: In some worlds, some propositions do not have a value of true or false.
(AT3) Pointed anti-trivialism (or minimal logical nihilism): In some worlds, every proposition does not have a value of true or false.
(AT4) Distributed anti-trivialism: In every world, some propositions do not have a value of true or false.
(AT5) Strong anti-trivialism: Some propositions do not have a value of true or false in every world.
(AT6) Super anti-trivialism (or moderate logical nihilism): All propositions do not have a value of true or false at some world.
(AT7) Absolute anti-trivialism (or maximal logical nihilism): All propositions do not have a value of true or false in every world.[3]

See also

Template:Portal

References

Template:Reflist

Further reading

Template:Wikiquote Template:Commons

Template:Logic Template:Philosophy topics

  1. ↑ Template:Cite book
  2. ↑ 2.0 2.1 2.2 2.3 Template:Cite book
  3. ↑ 3.0 3.1 3.2 3.3 3.4 Template:Cite journal
  4. ↑ 4.0 4.1 4.2 4.3 4.4 Template:Cite web
  5. ↑ Template:Cite journal
  6. ↑ 6.0 6.1 6.2 Template:Cite book
  7. ↑ Template:Cite journal
  8. ↑ Empiricus, S. (2000). Sextus Empiricus: Outlines of Scepticism. Cambridge University Press. "Suspension of judgement is a standstill of intellect, owing to which we neither reject nor posit anything" (p. 5).
  9. ↑ Template:Cite web
  10. ↑ Comesaña, J. (2012). Can Contemporary Semantics Help the Pyrrhonian Get a Life?. In Pyrrhonism in Ancient, Modern, and Contemporary Philosophy (pp. 217-240). Springer Netherlands.
  11. ↑ Wieland, J. W. (2012) Can Pyrrhonists act normally? Philosophical Explorations: An International Journal for the Philosophy of Mind and Action 15(3):277-289.
  12. ↑ Burnyeat, M. (1980). Can the sceptic live his scepticism?. In M. Schofield, M. Burnyeat, and J. Barnes (eds.), Doubt and Dogmatism (pp. 20-53). Cambridge University Press.
  13. ↑ Kabay, P.D. (2008) A Defense of Trivialism. Phd Thesis, School of Philosophy, Anthropology, and Social Inquiry, The University of Melbourne pages 32–35
  14. ↑ Kabay, pages 36–37
  15. ↑ Kabay, pages 37–40
  16. ↑ Kabay, pages 40–41. A Defense of Trivialism
  17. ↑ Template:Cite web
  18. ↑ Template:Cite journal
  19. ↑ Template:Cite journal
Retrieved from "https://en.beta.math.wmflabs.org/index.php?title=Trivialism&oldid=2473"