Mersenne prime

From testwiki
Jump to navigation Jump to search

Template:Short description Template:Infobox integer sequence In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form Template:Math for some integer Template:Math. They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17th century.

The exponents Template:Math which give Mersenne primes are 2, 3, 5, 7, 13, 17, 19, 31, ... Template:OEIS and the resulting Mersenne primes are 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, ... Template:OEIS.

If Template:Math is a composite number then so is Template:Math. (Template:Math is divisible by both Template:Math and Template:Math.) This definition is therefore equivalent to the definition as a prime number of the form Template:Math for some prime Template:Math.

More generally, numbers of the form Template:Math without the primality requirement may be called Mersenne numbers. Sometimes, however, Mersenne numbers are defined to have the additional requirement that Template:Math be prime. The smallest composite Mersenne number with prime exponent n is Template:Nowrap.

Mersenne primes Template:Math are also noteworthy due to their connection to perfect numbers.

Template:As of, 51 Mersenne primes are known. The largest known prime number, Template:Nowrap, is a Mersenne prime.[1] Since 1997, all newly found Mersenne primes have been discovered by the Great Internet Mersenne Prime Search (GIMPS), a distributed computing project on the Internet.

About Mersenne primes

Template:Unsolved Many fundamental questions about Mersenne primes remain unresolved. It is not even known whether the set of Mersenne primes is finite or infinite. The Lenstra–Pomerance–Wagstaff conjecture asserts that there are infinitely many Mersenne primes and predicts their order of growth. It is also not known whether infinitely many Mersenne numbers with prime exponents are composite, although this would follow from widely believed conjectures about prime numbers, for example, the infinitude of Sophie Germain primes congruent to 3 (mod 4). For these primes Template:Math, Template:Math (which is also prime) will divide Template:Math, for example, Template:Math, Template:Math, Template:Math, Template:Math, Template:Math, Template:Math, Template:Math, and Template:Math Template:OEIS. Since for these primes Template:Math, Template:Math is congruent to 7 mod 8, so 2 is a quadratic residue mod Template:Math, and the multiplicative order of 2 mod Template:Math must divide = Template:Math. Since Template:Math is a prime, it must be Template:Math or 1. However, it cannot be 1 since and 1 has no prime factors, so it must be Template:Math. Hence, Template:Math divides and cannot be prime.

The first four Mersenne primes are Template:Math, Template:Math, Template:Math and Template:Math and because the first Mersenne prime starts at Template:Math, all Mersenne primes are congruent to 3 (mod 4). Other than Template:Math and Template:Math, all other Mersenne numbers are also congruent to 3 (mod 4). Consequently, in the prime factorization of a Mersenne number ( Template:Math ) there must be at least one prime factor congruent to 3 (mod 4).

A basic theorem about Mersenne numbers states that if Template:Math is prime, then the exponent Template:Math must also be prime. This follows from the identity

This rules out primality for Mersenne numbers with composite exponent, such as Template:Math.

Though the above examples might suggest that Template:Math is prime for all primes Template:Math, this is not the case, and the smallest counterexample is the Mersenne number

Template:Math.

The evidence at hand suggests that a randomly selected Mersenne number is much more likely to be prime than an arbitrary randomly selected odd integer of similar size.[2] Nonetheless, prime values of Template:Math appear to grow increasingly sparse as Template:Math increases. For example, eight of the first 11 primes Template:Mvar give rise to a Mersenne prime Template:Math (the correct terms on Mersenne's original list), while Template:Math is prime for only 43 of the first two million prime numbers (up to 32,452,843).

The lack of any simple test to determine whether a given Mersenne number is prime makes the search for Mersenne primes a difficult task, since Mersenne numbers grow very rapidly. The Lucas–Lehmer primality test (LLT) is an efficient primality test that greatly aids this task, making it much easier to test the primality of Mersenne numbers than that of most other numbers of the same size. The search for the largest known prime has somewhat of a cult following. Consequently, a lot of computer power has been expended searching for new Mersenne primes, much of which is now done using distributed computing.

Mersenne primes are used in pseudorandom number generators such as the Mersenne twister, Park–Miller random number generator, Generalized Shift Register and Fibonacci RNG. They are also used in primitive trinomials, which can also be used to create PRNGs with very large periods.

Perfect numbers

Template:Main Mersenne primes Template:Math are also noteworthy due to their connection with perfect numbers. In the 4th century BC, Euclid proved that if Template:Math is prime, then Template:Math) is a perfect number. This number, also expressible as Template:Math, is the Template:Mathth triangular number and the Template:Mathth hexagonal number. In the 18th century, Leonhard Euler proved that, conversely, all even perfect numbers have this form.[3] This is known as the Euclid–Euler theorem. It is unknown whether there are any odd perfect numbers.

History

2 3 5 7 11 13 17 19
23 29 31 37 41 43 47 53
59 61 67 71 73 79 83 89
97 101 103 107 109 113 127 131
137 139 149 151 157 163 167 173
179 181 191 193 197 199 211 223
227 229 233 239 241 251 257 263
269 271 277 281 283 293 307 311
The first 64 prime exponents with those corresponding to Mersenne primes shaded in cyan and in bold, and those thought to do so by Mersenne in red and bold.

Mersenne primes take their name from the 17th-century French scholar Marin Mersenne, who compiled what was supposed to be a list of Mersenne primes with exponents up to 257. The exponents listed by Mersenne were as follows:

2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257.

His list replicated the known primes of his time with exponents up to 19. His next entry, 31, was correct, but the list then became largely incorrect, as Mersenne mistakenly included Template:Math and Template:Math (which are composite) and omitted Template:Math, Template:Math, and Template:Math (which are prime). Mersenne gave little indication how he came up with his list.[4]

Édouard Lucas proved in 1876 that Template:Math is indeed prime, as Mersenne claimed. This was the largest known prime number for 75 years, and the largest ever found by hand. Template:Math was determined to be prime in 1883 by Ivan Mikheevich Pervushin, though Mersenne claimed it was composite, and for this reason it is sometimes called Pervushin's number. This was the second-largest known prime number, and it remained so until 1911. Lucas had shown another error in Mersenne's list in 1876. Without finding a factor, Lucas demonstrated that Template:Math is actually composite. No factor was found until a famous talk by Frank Nelson Cole in 1903.[5] Without speaking a word, he went to a blackboard and raised 2 to the 67th power, then subtracted one. On the other side of the board, he multiplied Template:Nowrap and got the same number, then returned to his seat (to applause) without speaking.[6] He later said that the result had taken him "three years of Sundays" to find.[7] A correct list of all Mersenne primes in this number range was completed and rigorously verified only about three centuries after Mersenne published his list.

Searching for Mersenne primes

Fast algorithms for finding Mersenne primes are available, and Template:As of the seven largest known prime numbers are Mersenne primes.

The first four Mersenne primes Template:Math, Template:Math, Template:Math and Template:Math were known in antiquity. The fifth, Template:Math, was discovered anonymously before 1461; the next two (Template:Math and Template:Math) were found by Pietro Cataldi in 1588. After nearly two centuries, Template:Math was verified to be prime by Leonhard Euler in 1772. The next (in historical, not numerical order) was Template:Math, found by Édouard Lucas in 1876, then Template:Math by Ivan Mikheevich Pervushin in 1883. Two more (Template:Math and Template:Math) were found early in the 20th century, by R. E. Powers in 1911 and 1914, respectively.

The best method presently known for testing the primality of Mersenne numbers is the Lucas–Lehmer primality test. Specifically, it can be shown that for prime Template:Math, Template:Math is prime if and only if Template:Math divides Template:Math, where Template:Math and Template:Math for Template:Math.

During the era of manual calculation, all the exponents up to and including 257 were tested with the Lucas–Lehmer test and found to be composite. A notable contribution was made by retired Yale physics professor Horace Scudder Uhler, who did the calculations for exponents 157, 167, 193, 199, 227, and 229.[8] Unfortunately for those investigators, the interval they were testing contains the largest known relative gap between Mersenne primes; in relative terms: the next Mersenne prime exponent, 521, would turn out to be more than four times larger than the previous record of 127.

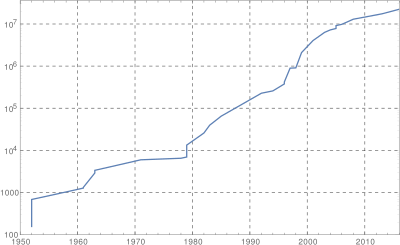
Graph of number of digits in largest known Mersenne prime by year – electronic era. Note that the vertical scale, the number of digits, is doubly logarithmic in the value of the prime.

The search for Mersenne primes was revolutionized by the introduction of the electronic digital computer. Alan Turing searched for them on the Manchester Mark 1 in 1949,[9] but the first successful identification of a Mersenne prime, Template:Math, by this means was achieved at 10:00 pm on January 30, 1952 using the U.S. National Bureau of Standards Western Automatic Computer (SWAC) at the Institute for Numerical Analysis at the University of California, Los Angeles, under the direction of Lehmer, with a computer search program written and run by Prof. R. M. Robinson. It was the first Mersenne prime to be identified in thirty-eight years; the next one, Template:Math, was found by the computer a little less than two hours later. Three more — Template:Math, Template:Math, Template:Math — were found by the same program in the next several months. Template:Math is the first Mersenne prime that is titanic, Template:Math is the first gigantic, and Template:Math was the first megaprime to be discovered, being a prime with at least 1,000,000 digits.[10] All three were the first known prime of any kind of that size. The number of digits in the decimal representation of Template:Math equals Template:Math, where Template:Math denotes the floor function (or equivalently Template:Math).

In September 2008, mathematicians at UCLA participating in GIMPS won part of a $100,000 prize from the Electronic Frontier Foundation for their discovery of a very nearly 13-million-digit Mersenne prime. The prize, finally confirmed in October 2009, is for the first known prime with at least 10 million digits. The prime was found on a Dell OptiPlex 745 on August 23, 2008. This was the eighth Mersenne prime discovered at UCLA.[11]

On April 12, 2009, a GIMPS server log reported that a 47th Mersenne prime had possibly been found. The find was first noticed on June 4, 2009, and verified a week later. The prime is Template:Nowrap. Although it is chronologically the 47th Mersenne prime to be discovered, it is smaller than the largest known at the time, which was the 45th to be discovered.

On January 25, 2013, Curtis Cooper, a mathematician at the University of Central Missouri, discovered a 48th Mersenne prime, Template:Nowrap (a number with 17,425,170 digits), as a result of a search executed by a GIMPS server network.[12]

On January 19, 2016, Cooper published his discovery of a 49th Mersenne prime, Template:Nowrap (a number with 22,338,618 digits), as a result of a search executed by a GIMPS server network.[13][14][15] This was the fourth Mersenne prime discovered by Cooper and his team in the past ten years.

On September 2, 2016, the Great Internet Mersenne Prime Search finished verifying all tests below M37,156,667, thus officially confirming its position as the 45th Mersenne prime.[16]

On January 3, 2018, it was announced that Jonathan Pace, a 51-year-old electrical engineer living in Germantown, Tennessee, had found a 50th Mersenne prime, Template:Nowrap (a number with 23,249,425 digits), as a result of a search executed by a GIMPS server network.[17]

On December 21, 2018, it was announced that The Great Internet Mersenne Prime Search (GIMPS) discovered the largest known prime number, Template:Nowrap, having 24,862,048 digits. A computer volunteered by Patrick Laroche from Ocala, Florida made the find on December 7, 2018.[18]

Theorems about Mersenne numbers

  1. If Template:Math and Template:Math are natural numbers such that Template:Math is prime, then Template:Math or Template:Math.
  2. If Template:Math is prime, then Template:Math is prime.
  3. If Template:Math is an odd prime, then every prime Template:Math that divides Template:Math must be 1 plus a multiple of Template:Math. This holds even when Template:Math is prime.
  4. If Template:Math is an odd prime, then every prime Template:Math that divides Template:Math is congruent to Template:Nowrap.
  5. A Mersenne prime cannot be a Wieferich prime.
  6. If Template:Math and Template:Math are natural numbers then Template:Math and Template:Math are coprime if and only if Template:Math and Template:Math are coprime. Consequently, a prime number divides at most one prime-exponent Mersenne number,[19] so in other words the set of pernicious Mersenne numbers is pairwise coprime.
  7. If Template:Math and Template:Math are both prime (meaning that Template:Math is a Sophie Germain prime), and Template:Math is congruent to Template:Nowrap, then Template:Math divides Template:Math.[20]
  8. All composite divisors of prime-exponent Mersenne numbers are strong pseudoprimes to the base 2.
  9. With the exception of 1, a Mersenne number cannot be a perfect power. In other words, and in accordance with Mihăilescu's theorem, the equation 2m-1 = nk has no solutions where m, n, and k are integers with m > 1 and k > 1.

List of known Mersenne primes

The table below lists all known Mersenne primes (sequence Template:OEIS link (Template:Math) and Template:OEIS link (Template:Math) in OEIS):

# Template:Math Template:Math Template:Math digits Discovered Discoverer Method used
1 2 3 1 c. 430 BC Ancient Greek mathematicians[21]
2 3 7 1 c. 430 BC Ancient Greek mathematicians[21]
3 5 31 2 c. 300 BC Ancient Greek mathematicians[22]
4 7 127 3 c. 300 BC Ancient Greek mathematicians[22]
5 13 8191 4 1456 Anonymous[23][24] Trial division
6 17 131071 6 1588[25] Pietro Cataldi Trial division[26]
7 19 524287 6 1588 Pietro Cataldi Trial division[27]
8 31 2147483647 10 1772 Leonhard Euler[28][29] Trial division with modular restrictions[30]
9 61 2305843009213693951 19 1883 November[31] Ivan M. Pervushin Lucas sequences
10 89 618970019642...137449562111 27 1911 June[32] Ralph Ernest Powers Lucas sequences
11 107 162259276829...578010288127 33 1914 June 1[33][34][35] Ralph Ernest Powers[36] Lucas sequences
12 127 170141183460...715884105727 39 1876 January 10[37] Édouard Lucas Lucas sequences
13 521 686479766013...291115057151 157 1952 January 30[38] Raphael M. Robinson LLT / SWAC
14 607 531137992816...219031728127 183 1952 January 30[38] Raphael M. Robinson LLT / SWAC
15 1,279 104079321946...703168729087 386 1952 June 25[39] Raphael M. Robinson LLT / SWAC
16 2,203 147597991521...686697771007 664 1952 October 7[40] Raphael M. Robinson LLT / SWAC
17 2,281 446087557183...418132836351 687 1952 October 9[40] Raphael M. Robinson LLT / SWAC
18 3,217 259117086013...362909315071 969 1957 September 8[41] Hans Riesel LLT / BESK
19 4,253 190797007524...815350484991 1,281 1961 November 3[42][43] Alexander Hurwitz LLT / IBM 7090
20 4,423 285542542228...902608580607 1,332 1961 November 3[42][43] Alexander Hurwitz LLT / IBM 7090
21 9,689 478220278805...826225754111 2,917 1963 May 11[44] Donald B. Gillies LLT / ILLIAC II
22 9,941 346088282490...883789463551 2,993 1963 May 16[44] Donald B. Gillies LLT / ILLIAC II
23 11,213 281411201369...087696392191 3,376 1963 June 2[44] Donald B. Gillies LLT / ILLIAC II
24 19,937 431542479738...030968041471 6,002 1971 March 4[45] Bryant Tuckerman LLT / IBM 360/91
25 21,701 448679166119...353511882751 6,533 1978 October 30[46] Landon Curt Noll & Laura Nickel LLT / CDC Cyber 174
26 23,209 402874115778...523779264511 6,987 1979 February 9[47] Landon Curt Noll LLT / CDC Cyber 174
27 44,497 854509824303...961011228671 13,395 1979 April 8[48][49] Harry L. Nelson & David Slowinski LLT / Cray 1
28 86,243 536927995502...709433438207 25,962 1982 September 25 David Slowinski LLT / Cray 1
29 110,503 521928313341...083465515007 33,265 1988 January 29[50][51] Walter Colquitt & Luke Welsh LLT / NEC SX-2[52]
30 132,049 512740276269...455730061311 39,751 1983 September 19[53] David Slowinski LLT / Cray X-MP
31 216,091 746093103064...103815528447 65,050 1985 September 1[54][55] David Slowinski LLT / Cray X-MP/24
32 756,839 174135906820...328544677887 227,832 1992 February 17 David Slowinski & Paul Gage LLT / Harwell Lab's Cray-2[56]
33 859,433 129498125604...243500142591 258,716 1994 January 4[57][58][59] David Slowinski & Paul Gage LLT / Cray C90
34 1,257,787 412245773621...976089366527 378,632 1996 September 3[60] David Slowinski & Paul Gage[61] LLT / Cray T94
35 1,398,269 814717564412...868451315711 420,921 1996 November 13 GIMPS / Joel Armengaud[62] LLT / Prime95 on 90 MHz Pentium
36 2,976,221 623340076248...743729201151 895,932 1997 August 24 GIMPS / Gordon Spence[63] LLT / Prime95 on 100 MHz Pentium
37 3,021,377 127411683030...973024694271 909,526 1998 January 27 GIMPS / Roland Clarkson[64] LLT / Prime95 on 200 MHz Pentium
38 6,972,593 437075744127...142924193791 2,098,960 1999 June 1 GIMPS / Nayan Hajratwala[65] LLT / Prime95 on 350 MHz Pentium II IBM Aptiva
39 13,466,917 924947738006...470256259071 4,053,946 2001 November 14 GIMPS / Michael Cameron[66] LLT / Prime95 on 800 MHz Athlon T-Bird
40 20,996,011 125976895450...762855682047 6,320,430 2003 November 17 GIMPS / Michael Shafer[67] LLT / Prime95 on 2 GHz Dell Dimension
41 24,036,583 299410429404...882733969407 7,235,733 2004 May 15 GIMPS / Josh Findley[68] LLT / Prime95 on 2.4 GHz Pentium 4
42 25,964,951 122164630061...280577077247 7,816,230 2005 February 18 GIMPS / Martin Nowak[69] LLT / Prime95 on 2.4 GHz Pentium 4
43 30,402,457 315416475618...411652943871 9,152,052 2005 December 15 GIMPS / Curtis Cooper & Steven Boone[70] LLT / Prime95 on 2 GHz Pentium 4
44 32,582,657 124575026015...154053967871 9,808,358 2006 September 4 GIMPS / Curtis Cooper & Steven Boone[71] LLT / Prime95 on 3 GHz Pentium 4
45 37,156,667 202254406890...022308220927 11,185,272 2008 September 6 GIMPS / Hans-Michael Elvenich[72] LLT / Prime95 on 2.83 GHz Core 2 Duo
46 42,643,801 169873516452...765562314751 12,837,064 2009 June 4[n 1] GIMPS / Odd M. Strindmo[73][n 2] LLT / Prime95 on 3 GHz Core 2
47 43,112,609 316470269330...166697152511 12,978,189 2008 August 23 GIMPS / Edson Smith[72] LLT / Prime95 on Dell Optiplex 745
48[n 3] 57,885,161 581887266232...071724285951 17,425,170 2013 January 25 GIMPS / Curtis Cooper[74] LLT / Prime95 on 3 GHz Intel Core2 Duo E8400[75]
49[n 3] 74,207,281 300376418084...391086436351 22,338,618 2016 January 7[n 4] GIMPS / Curtis Cooper[13] LLT / Prime95 on Intel Core i7-4790
50[n 3] 77,232,917 467333183359...069762179071 23,249,425 2017 December 26 GIMPS / Jon Pace[76] LLT / Prime95 on 3.3 GHz Intel Core i5-6600[77]
51[n 3] 82,589,933 148894445742...325217902591 24,862,048 2018 December 7 GIMPS / Patrick Laroche[1] LLT / Prime95 on Intel Core i5-4590T
  1. ↑ Although Template:Math was first reported by a machine on April 12, 2009, no human took notice of this fact until June 4, 2009.
  2. ↑ Strindmo also uses the alias Stig M. Valstad.
  3. ↑ 3.0 3.1 3.2 3.3 It is not verified whether any undiscovered Mersenne primes exist between the 47th (Template:Math) and the 51st (Template:Math) on this chart; the ranking is therefore provisional.
  4. ↑ Although Template:Math was first reported by a machine on September 17, 2015, no human took notice of this fact until January 7, 2016.

All Mersenne numbers below the 51st Mersenne prime (Template:Math) have been tested at least once but some have not been double-checked. Primes are not always discovered in increasing order. For example, the 29th Mersenne prime was discovered after the 30th and the 31st. Similarly, Template:Math was followed by two smaller Mersenne primes, first 2 weeks later and then 9 months later.[78] Template:Math was the first discovered prime number with more than 10 million decimal digits.

The largest known Mersenne prime Template:Nowrap is also the largest known prime number.[1]

The largest known prime has been a Mersenne prime since 1952, except between 1989 and 1992.[79]

Factorization of composite Mersenne numbers

Since they are prime numbers, Mersenne primes are divisible only by 1 and by themselves. However, not all Mersenne numbers are Mersenne primes, and the composite Mersenne numbers may be factored non-trivially. Mersenne numbers are very good test cases for the special number field sieve algorithm, so often the largest number factorized with this algorithm has been a Mersenne number. Template:As of, 2Template:Sup − 1 is the record-holder,[80] having been factored with a variant of the special number field sieve that allows the factorization of several numbers at once. See integer factorization records for links to more information. The special number field sieve can factorize numbers with more than one large factor. If a number has only one very large factor then other algorithms can factorize larger numbers by first finding small factors and then making a primality test on the cofactor. Template:As of, the largest factorization with probable prime factors allowed is Template:Nowrap, where Template:Math is a 2,201,714-digit probable prime. It was discovered by Oliver Kruse.[81] Template:As of, the Mersenne number M1277 is the smallest composite Mersenne number with no known factors; it has no prime factors below 267.[82]

The table below shows factorizations for the first 20 composite Mersenne numbers Template:OEIS.

Template:Math Template:Math Factorization of Template:Math
11 2047 23 × 89
23 8388607 47 × 178,481
29 536870911 233 × 1,103 × 2,089
37 137438953471 223 × 616,318,177
41 2199023255551 13,367 × 164,511,353
43 8796093022207 431 × 9,719 × 2,099,863
47 140737488355327 2,351 × 4,513 × 13,264,529
53 9007199254740991 6,361 × 69,431 × 20,394,401
59 57646075230343487 179,951 × 3,203,431,780,337 (13 digits)
67 147573952589676412927 193,707,721 × 761,838,257,287 (12 digits)
71 2361183241434822606847 228,479 × 48,544,121 × 212,885,833
73 9444732965739290427391 439 × 2,298,041 × 9,361,973,132,609 (13 digits)
79 604462903807314587353087 2,687 × 202,029,703 × 1,113,491,139,767 (13 digits)
83 967140655691...033397649407 167 × 57,912,614,113,275,649,087,721 (23 digits)
97 158456325028...187087900671 11,447 × 13,842,607,235,828,485,645,766,393 (26 digits)
101 253530120045...993406410751 7,432,339,208,719 (13 digits) × 341,117,531,003,194,129 (18 digits)
103 101412048018...973625643007 2,550,183,799 × 3,976,656,429,941,438,590,393 (22 digits)
109 649037107316...312041152511 745,988,807 × 870,035,986,098,720,987,332,873 (24 digits)
113 103845937170...992658440191 3,391 × 23,279 × 65,993 × 1,868,569 × 1,066,818,132,868,207 (16 digits)
131 272225893536...454145691647 263 × 10,350,794,431,055,162,386,718,619,237,468,234,569 (38 digits)

The number of factors for the first 500 Mersenne numbers can be found at Template:OEIS.

Mersenne numbers in nature and elsewhere

In the mathematical problem Tower of Hanoi, solving a puzzle with an Template:Math-disc tower requires Template:Math steps, assuming no mistakes are made.[83] The number of rice grains on the whole chessboard in the wheat and chessboard problem is Template:Math.

The asteroid with minor planet number 8191 is named 8191 Mersenne after Marin Mersenne, because 8191 is a Mersenne prime (3 Juno, 7 Iris, 31 Euphrosyne and 127 Johanna having been discovered and named during the 19th century).[84]

In geometry, an integer right triangle that is primitive and has its even leg a power of 2 ( Template:Math ) generates a unique right triangle such that its inradius is always a Mersenne number. For example, if the even leg is Template:Math then because it is primitive it constrains the odd leg to be Template:Math, the hypotenuse to be Template:Math and its inradius to be Template:Math.[85]

The Mersenne numbers were studied with respect to the total number of accepting paths of non-deterministic polynomial time Turing machines in 2018[86] and intriguing inclusions were discovered.

Mersenne–Fermat primes

A Mersenne–Fermat number is defined as Template:Math, with Template:Math prime, Template:Math natural number, and can be written as Template:Math, when Template:Math, it is a Mersenne number, and when Template:Math, it is a Fermat number, the only known Mersenne–Fermat prime with Template:Math are

Template:Math and Template:Math.[87]

In fact, Template:Math, where Template:Math is the cyclotomic polynomial.

Generalizations

The simplest generalized Mersenne primes are prime numbers of the form Template:Math, where Template:Math is a low-degree polynomial with small integer coefficients.[88] An example is Template:Math, in this case, Template:Math, and Template:Math; another example is Template:Math, in this case, Template:Math, and Template:Math.

It is also natural to try to generalize primes of the form Template:Math to primes of the form Template:Math (for Template:Math and Template:Math). However (see also theorems above), Template:Math is always divisible by Template:Math, so unless the latter is a unit, the former is not a prime. This can be remedied by allowing b to be an algebraic integer instead of an integer:

Complex numbers

In the ring of integers (on real numbers), if Template:Math is a unit, then Template:Math is either 2 or 0. But Template:Math are the usual Mersenne primes, and the formula Template:Math does not lead to anything interesting (since it is always −1 for all Template:Math). Thus, we can regard a ring of "integers" on complex numbers instead of real numbers, like Gaussian integers and Eisenstein integers.

Gaussian Mersenne primes

If we regard the ring of Gaussian integers, we get the case Template:Math and Template:Math, and can ask (WLOG) for which Template:Math the number Template:Math is a Gaussian prime which will then be called a Gaussian Mersenne prime.[89]

Template:Math is a Gaussian prime for the following Template:Math:

2, 3, 5, 7, 11, 19, 29, 47, 73, 79, 113, 151, 157, 163, 167, 239, 241, 283, 353, 367, 379, 457, 997, 1367, 3041, 10141, 14699, 27529, 49207, 77291, 85237, 106693, 160423, 203789, 364289, 991961, 1203793, 1667321, 3704053, 4792057, ... Template:OEIS

Like the sequence of exponents for usual Mersenne primes, this sequence contains only (rational) prime numbers.

As for all Gaussian primes, the norms (that is, squares of absolute values) of these numbers are rational primes:

5, 13, 41, 113, 2113, 525313, 536903681, 140737471578113, ... Template:OEIS.

Eisenstein Mersenne primes

We can also regard the ring of Eisenstein integers, we get the case Template:Math and Template:Math, and can ask for what Template:Math the number Template:Math is an Eisenstein prime which will then be called a Eisenstein Mersenne prime.

Template:Math is an Eisenstein prime for the following Template:Math:

2, 5, 7, 11, 17, 19, 79, 163, 193, 239, 317, 353, 659, 709, 1049, 1103, 1759, 2029, 5153, 7541, 9049, 10453, 23743, 255361, 534827, 2237561, ... Template:OEIS

The norms (that is, squares of absolute values) of these Eisenstein primes are rational primes:

7, 271, 2269, 176419, 129159847, 1162320517, ... Template:OEIS

Divide an integer

Repunit primes

Template:Main The other way to deal with the fact that Template:Math is always divisible by Template:Math, it is to simply take out this factor and ask which values of Template:Math make

be prime. (The integer Template:Math can be either positive or negative.) If, for example, we take Template:Math, we get Template:Math values of:

2, 19, 23, 317, 1031, 49081, 86453, 109297, 270343, ... Template:OEIS,
corresponding to primes 11, 1111111111111111111, 11111111111111111111111, ... Template:OEIS.

These primes are called repunit primes. Another example is when we take Template:Math, we get Template:Math values of:

2, 5, 11, 109, 193, 1483, 11353, 21419, 21911, 24071, 106859, 139739, ... Template:OEIS,
corresponding to primes −11, 19141, 57154490053, ....

It is a conjecture that for every integer Template:Math which is not a perfect power, there are infinitely many values of Template:Math such that Template:Math is prime. (When Template:Math is a perfect power, it can be shown that there is at most one Template:Math value such that Template:Math is prime)

Least Template:Math such that Template:Math is prime are (starting with Template:Math, Template:Math if no such Template:Math exists)

2, 3, 2, 3, 2, 5, 3, 0, 2, 17, 2, 5, 3, 3, 2, 3, 2, 19, 3, 3, 2, 5, 3, 0, 7, 3, 2, 5, 2, 7, 0, 3, 13, 313, 2, 13, 3, 349, 2, 3, 2, 5, 5, 19, 2, 127, 19, 0, 3, 4229, 2, 11, 3, 17, 7, 3, 2, 3, 2, 7, 3, 5, 0, 19, 2, 19, 5, 3, 2, 3, 2, ... Template:OEIS

For negative bases Template:Math, they are (starting with Template:Math, Template:Math if no such Template:Math exists)

3, 2, 2, 5, 2, 3, 2, 3, 5, 5, 2, 3, 2, 3, 3, 7, 2, 17, 2, 3, 3, 11, 2, 3, 11, 0, 3, 7, 2, 109, 2, 5, 3, 11, 31, 5, 2, 3, 53, 17, 2, 5, 2, 103, 7, 5, 2, 7, 1153, 3, 7, 21943, 2, 3, 37, 53, 3, 17, 2, 7, 2, 3, 0, 19, 7, 3, 2, 11, 3, 5, 2, ... Template:OEIS (notice this OEIS sequence does not allow Template:Math)

Least base Template:Math such that Template:Math is prime are

2, 2, 2, 2, 5, 2, 2, 2, 10, 6, 2, 61, 14, 15, 5, 24, 19, 2, 46, 3, 11, 22, 41, 2, 12, 22, 3, 2, 12, 86, 2, 7, 13, 11, 5, 29, 56, 30, 44, 60, 304, 5, 74, 118, 33, 156, 46, 183, 72, 606, 602, 223, 115, 37, 52, 104, 41, 6, 338, 217, ... Template:OEIS

For negative bases Template:Math, they are

3, 2, 2, 2, 2, 2, 2, 2, 2, 7, 2, 16, 61, 2, 6, 10, 6, 2, 5, 46, 18, 2, 49, 16, 70, 2, 5, 6, 12, 92, 2, 48, 89, 30, 16, 147, 19, 19, 2, 16, 11, 289, 2, 12, 52, 2, 66, 9, 22, 5, 489, 69, 137, 16, 36, 96, 76, 117, 26, 3, ... Template:OEIS

Other generalized Mersenne primes

Another generalized Mersenne number is

with Template:Math, Template:Math any coprime integers, Template:Math and Template:Math. (Since Template:Math is always divisible by Template:Math, the division is necessary for there to be any chance of finding prime numbers. In fact, this number is the same as the Lucas number Template:Math, since Template:Math and Template:Math are the roots of the quadratic equation Template:Math, and this number equals 1 when Template:Math) We can ask which Template:Math makes this number prime. It can be shown that such Template:Math must be primes themselves or equal to 4, and Template:Math can be 4 if and only if Template:Math and Template:Math is prime. (Since Template:Math. Thus, in this case the pair Template:Math must be Template:Math and Template:Math must be prime. That is, Template:Math must be in Template:Oeis.) It is a conjecture that for any pair Template:Math such that for every natural number Template:Math, Template:Math and Template:Math are not both perfect Template:Mathth powers, and Template:Math is not a perfect fourth power. there are infinitely many values of Template:Math such that Template:Math is prime. (When Template:Math and Template:Math are both perfect Template:Mathth powers for an Template:Math or when Template:Math is a perfect fourth power, it can be shown that there are at most two Template:Math values with this property, since if so, then Template:Math can be factored algebraically) However, this has not been proved for any single value of Template:Math.

For more information, see [90][91][92][93][94][95][96][97][98][99]
Template:Math Template:Math numbers Template:Math such that Template:Math is prime
(some large terms are only probable primes, these Template:Math are checked up to 100000 for Template:Math or Template:Math, 20000 for Template:Math) 		OEIS sequence
2 1 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801, 43112609, ..., 57885161, ..., 74207281, ..., 77232917, ..., 82589933, ... Template:OEIS link
2 −1 3, 4*, 5, 7, 11, 13, 17, 19, 23, 31, 43, 61, 79, 101, 127, 167, 191, 199, 313, 347, 701, 1709, 2617, 3539, 5807, 10501, 10691, 11279, 12391, 14479, 42737, 83339, 95369, 117239, 127031, 138937, 141079, 267017, 269987, 374321, 986191, 4031399, ..., 13347311, 13372531, ... Template:OEIS link
3 2 2, 3, 5, 17, 29, 31, 53, 59, 101, 277, 647, 1061, 2381, 2833, 3613, 3853, 3929, 5297, 7417, 90217, 122219, 173191, 256199, 336353, 485977, 591827, 1059503, ... Template:OEIS link
3 1 3, 7, 13, 71, 103, 541, 1091, 1367, 1627, 4177, 9011, 9551, 36913, 43063, 49681, 57917, 483611, 877843, ... Template:OEIS link
3 −1 2*, 3, 5, 7, 13, 23, 43, 281, 359, 487, 577, 1579, 1663, 1741, 3191, 9209, 11257, 12743, 13093, 17027, 26633, 104243, 134227, 152287, 700897, 1205459, ... Template:OEIS link
3 −2 3, 4*, 7, 11, 83, 149, 223, 599, 647, 1373, 8423, 149497, 388897, ... Template:OEIS link
4 3 2, 3, 7, 17, 59, 283, 311, 383, 499, 521, 541, 599, 1193, 1993, 2671, 7547, 24019, 46301, 48121, 68597, 91283, 131497, 148663, 184463, 341233, ... Template:OEIS link
4 1 2 (no others)
4 −1 2*, 3 (no others)
4 −3 3, 5, 19, 37, 173, 211, 227, 619, 977, 1237, 2437, 5741, 13463, 23929, 81223, 121271, ... Template:OEIS link
5 4 3, 43, 59, 191, 223, 349, 563, 709, 743, 1663, 5471, 17707, 19609, 35449, 36697, 45259, 91493, 246497, 265007, 289937, ... Template:OEIS link
5 3 13, 19, 23, 31, 47, 127, 223, 281, 2083, 5281, 7411, 7433, 19051, 27239, 35863, 70327, ... Template:OEIS link
5 2 2, 5, 7, 13, 19, 37, 59, 67, 79, 307, 331, 599, 1301, 12263, 12589, 18443, 20149, 27983, ... Template:OEIS link
5 1 3, 7, 11, 13, 47, 127, 149, 181, 619, 929, 3407, 10949, 13241, 13873, 16519, 201359, 396413, 1888279, ... Template:OEIS link
5 −1 5, 67, 101, 103, 229, 347, 4013, 23297, 30133, 177337, 193939, 266863, 277183, 335429, ... Template:OEIS link
5 −2 2*, 3, 17, 19, 47, 101, 1709, 2539, 5591, 6037, 8011, 19373, 26489, 27427, ... Template:OEIS link
5 −3 2*, 3, 5, 7, 17, 19, 109, 509, 661, 709, 1231, 12889, 13043, 26723, 43963, 44789, ... Template:OEIS link
5 −4 4*, 5, 7, 19, 29, 61, 137, 883, 1381, 1823, 5227, 25561, 29537, 300893, ... Template:OEIS link
6 5 2, 5, 11, 13, 23, 61, 83, 421, 1039, 1511, 31237, 60413, 113177, 135647, 258413, ... Template:OEIS link
6 1 2, 3, 7, 29, 71, 127, 271, 509, 1049, 6389, 6883, 10613, 19889, 79987, 608099, ... Template:OEIS link
6 −1 2*, 3, 11, 31, 43, 47, 59, 107, 811, 2819, 4817, 9601, 33581, 38447, 41341, 131891, 196337, ... Template:OEIS link
6 −5 3, 4*, 5, 17, 397, 409, 643, 1783, 2617, 4583, 8783, ... Template:OEIS link
7 6 2, 3, 7, 29, 41, 67, 1327, 1399, 2027, 69371, 86689, 355039, ... Template:OEIS link
7 5 3, 5, 7, 113, 397, 577, 7573, 14561, 58543, ... Template:OEIS link
7 4 2, 5, 11, 61, 619, 2879, 2957, 24371, 69247, ... Template:OEIS link
7 3 3, 7, 19, 109, 131, 607, 863, 2917, 5923, 12421, ... Template:OEIS link
7 2 3, 7, 19, 79, 431, 1373, 1801, 2897, 46997, ... Template:OEIS link
7 1 5, 13, 131, 149, 1699, 14221, 35201, 126037, 371669, 1264699, ... Template:OEIS link
7 −1 3, 17, 23, 29, 47, 61, 1619, 18251, 106187, 201653, ... Template:OEIS link
7 −2 2*, 5, 23, 73, 101, 401, 419, 457, 811, 1163, 1511, 8011, ... Template:OEIS link
7 −3 3, 13, 31, 313, 3709, 7933, 14797, 30689, 38333, ... Template:OEIS link
7 −4 2*, 3, 5, 19, 41, 47, 8231, 33931, 43781, 50833, 53719, 67211, ... Template:OEIS link
7 −5 2*, 11, 31, 173, 271, 547, 1823, 2111, 5519, 7793, 22963, 41077, 49739, ... Template:OEIS link
7 −6 3, 53, 83, 487, 743, ... Template:OEIS link
8 7 7, 11, 17, 29, 31, 79, 113, 131, 139, 4357, 44029, 76213, 83663, 173687, 336419, 615997, ... Template:OEIS link
8 5 2, 19, 1021, 5077, 34031, 46099, 65707, ... Template:OEIS link
8 3 2, 3, 7, 19, 31, 67, 89, 9227, 43891, ... Template:OEIS link
8 1 3 (no others)
8 −1 2* (no others)
8 −3 2*, 5, 163, 191, 229, 271, 733, 21059, 25237, ... Template:OEIS link
8 −5 2*, 7, 19, 167, 173, 223, 281, 21647, ... Template:OEIS link
8 −7 4*, 7, 13, 31, 43, 269, 353, 383, 619, 829, 877, 4957, 5711, 8317, 21739, 24029, 38299, ... Template:OEIS link
9 8 2, 7, 29, 31, 67, 149, 401, 2531, 19913, 30773, 53857, 170099, ... Template:OEIS link
9 7 3, 5, 7, 4703, 30113, ... Template:OEIS link
9 5 3, 11, 17, 173, 839, 971, 40867, 45821, ... Template:OEIS link
9 4 2 (no others)
9 2 2, 3, 5, 13, 29, 37, 1021, 1399, 2137, 4493, 5521, ... Template:OEIS link
9 1 (none)
9 −1 3, 59, 223, 547, 773, 1009, 1823, 3803, 49223, 193247, 703393, ... Template:OEIS link
9 −2 2*, 3, 7, 127, 283, 883, 1523, 4001, ... Template:OEIS link
9 −4 2*, 3, 5, 7, 11, 17, 19, 41, 53, 109, 167, 2207, 3623, 5059, 5471, 7949, 21211, 32993, 60251, ... Template:OEIS link
9 −5 3, 5, 13, 17, 43, 127, 229, 277, 6043, 11131, 11821, ... Template:OEIS link
9 −7 2*, 3, 107, 197, 2843, 3571, 4451, ..., 31517, ... Template:OEIS link
9 −8 3, 7, 13, 19, 307, 619, 2089, 7297, 75571, 76103, 98897, ... Template:OEIS link
10 9 2, 3, 7, 11, 19, 29, 401, 709, 2531, 15787, 66949, 282493, ... Template:OEIS link
10 7 2, 31, 103, 617, 10253, 10691, ... Template:OEIS link
10 3 2, 3, 5, 37, 599, 38393, 51431, ... Template:OEIS link
10 1 2, 19, 23, 317, 1031, 49081, 86453, 109297, 270343, ... Template:OEIS link
10 −1 5, 7, 19, 31, 53, 67, 293, 641, 2137, 3011, 268207, ... Template:OEIS link
10 −3 2*, 3, 19, 31, 101, 139, 167, 1097, 43151, 60703, 90499, ... Template:OEIS link
10 −7 2*, 3, 5, 11, 19, 1259, 1399, 2539, 2843, 5857, 10589, ...
10 −9 4*, 7, 67, 73, 1091, 1483, 10937, ... Template:OEIS link
11 10 3, 5, 19, 311, 317, 1129, 4253, 7699, 18199, 35153, 206081, ... Template:OEIS link
11 9 5, 31, 271, 929, 2789, 4153, ... Template:OEIS link
11 8 2, 7, 11, 17, 37, 521, 877, 2423, ... Template:OEIS link
11 7 5, 19, 67, 107, 593, 757, 1801, 2243, 2383, 6043, 10181, 11383, 15629, ... Template:OEIS link
11 6 2, 3, 11, 163, 191, 269, 1381, 1493, ... Template:OEIS link
11 5 5, 41, 149, 229, 263, 739, 3457, 20269, 98221, ... Template:OEIS link
11 4 3, 5, 11, 17, 71, 89, 827, 22307, 45893, 63521, ... Template:OEIS link
11 3 3, 5, 19, 31, 367, 389, 431, 2179, 10667, 13103, 90397, ... Template:OEIS link
11 2 2, 5, 11, 13, 331, 599, 18839, 23747, 24371, 29339, 32141, 67421, ... Template:OEIS link
11 1 17, 19, 73, 139, 907, 1907, 2029, 4801, 5153, 10867, 20161, 293831, ... Template:OEIS link
11 −1 5, 7, 179, 229, 439, 557, 6113, 223999, 327001, ... Template:OEIS link
11 −2 3, 5, 17, 67, 83, 101, 1373, 6101, 12119, 61781, ... Template:OEIS link
11 −3 3, 103, 271, 523, 23087, 69833, ... Template:OEIS link
11 −4 2*, 7, 53, 67, 71, 443, 26497, ... Template:OEIS link
11 −5 7, 11, 181, 421, 2297, 2797, 4129, 4139, 7151, 29033, ... Template:OEIS link
11 −6 2*, 5, 7, 107, 383, 17359, 21929, 26393, ...
11 −7 7, 1163, 4007, 10159, ...
11 −8 2*, 3, 13, 31, 59, 131, 223, 227, 1523, ...
11 −9 2*, 3, 17, 41, 43, 59, 83, ...
11 −10 53, 421, 647, 1601, 35527, ... Template:OEIS link
12 11 2, 3, 7, 89, 101, 293, 4463, 70067, ... Template:OEIS link
12 7 2, 3, 7, 13, 47, 89, 139, 523, 1051, ... Template:OEIS link
12 5 2, 3, 31, 41, 53, 101, 421, 1259, 4721, 45259, ... Template:OEIS link
12 1 2, 3, 5, 19, 97, 109, 317, 353, 701, 9739, 14951, 37573, 46889, 769543, ... Template:OEIS link
12 −1 2*, 5, 11, 109, 193, 1483, 11353, 21419, 21911, 24071, 106859, 139739, ... Template:OEIS link
12 −5 2*, 3, 5, 13, 347, 977, 1091, 4861, 4967, 34679, ... Template:OEIS link
12 −7 2*, 3, 7, 67, 79, 167, 953, 1493, 3389, 4871, ...
12 −11 47, 401, 509, 8609, ... Template:OEIS link

*Note: if Template:Math and Template:Math is even, then the numbers Template:Math are not included in the corresponding OEIS sequence.

A conjecture related to the generalized Mersenne primes:[2][100] (the conjecture predicts where is the next generalized Mersenne prime, if the conjecture is true, then there are infinitely many primes for all such Template:Math pairs)

For any integers Template:Math and Template:Math which satisfy the conditions:

  1. Template:Math, Template:Math.
  2. Template:Math and Template:Math are coprime. (thus, Template:Math cannot be 0)
  3. For every natural number Template:Math, Template:Math and Template:Math are not both perfect Template:Mathth powers. (since when Template:Math and Template:Math are both perfect Template:Mathth powers, it can be shown that there are at most two Template:Math value such that Template:Math is prime, and these Template:Math values are Template:Math itself or a root of Template:Math, or 2)
  4. Template:Math is not a perfect fourth power (if so, then the number has aurifeuillean factorization).

has prime numbers of the form

for prime Template:Math, the prime numbers will be distributed near the best fit line

where

and there are about

prime numbers of this form less than Template:Math.

We also have the following three properties:

  1. The number of prime numbers of the form Template:Math (with prime Template:Math) less than or equal to Template:Math is about Template:Math.
  2. The expected number of prime numbers of the form Template:Math with prime Template:Math between Template:Math and Template:Math is about Template:Math.
  3. The probability that number of the form Template:Math is prime (for prime Template:Math) is about Template:Math.

If this conjecture is true, then for all such Template:Math pairs, let Template:Math be the Template:Mathth prime of the form Template:Math, the graph of Template:Math versus Template:Math is almost linear. (See [2])

When Template:Math, it is Template:Math, a difference of two consecutive perfect Template:Mathth powers, and if Template:Math is prime, then Template:Math must be Template:Math, because it is divisible by Template:Math.

Least Template:Math such that Template:Math is prime are

2, 2, 2, 3, 2, 2, 7, 2, 2, 3, 2, 17, 3, 2, 2, 5, 3, 2, 5, 2, 2, 229, 2, 3, 3, 2, 3, 3, 2, 2, 5, 3, 2, 3, 2, 2, 3, 3, 2, 7, 2, 3, 37, 2, 3, 5, 58543, 2, 3, 2, 2, 3, 2, 2, 3, 2, 5, 3, 4663, 54517, 17, 3, 2, 5, 2, 3, 3, 2, 2, 47, 61, 19, ... Template:OEIS

Least Template:Math such that Template:Math is prime are

1, 1, 1, 1, 5, 1, 1, 1, 5, 2, 1, 39, 6, 4, 12, 2, 2, 1, 6, 17, 46, 7, 5, 1, 25, 2, 41, 1, 12, 7, 1, 7, 327, 7, 8, 44, 26, 12, 75, 14, 51, 110, 4, 14, 49, 286, 15, 4, 39, 22, 109, 367, 22, 67, 27, 95, 80, 149, 2, 142, 3, 11, ... Template:OEIS

See also

Template:Div col

Template:Div col end

References

Template:Reflist

External links

Template:Wiktionary Template:Wikinewspar2

MathWorld links

Template:Prime number classes Template:Classes of natural numbers Template:Mersenne Template:Large numbers

  1. ↑ 1.0 1.1 1.2 Template:Cite web
  2. ↑ 2.0 2.1 2.2 Template:Cite web
  3. ↑ Chris K. Caldwell, Mersenne Primes: History, Theorems and Lists
  4. ↑ The Prime Pages, Mersenne's conjecture.
  5. ↑ Template:Citation
  6. ↑ Template:Cite book p. 228.
  7. ↑ Template:Cite news
  8. ↑ Template:Cite journal
  9. ↑ Brian Napper, The Mathematics Department and the Mark 1.
  10. ↑ The Prime Pages, The Prime Glossary: megaprime.
  11. ↑ Template:Cite news
  12. ↑ Template:Cite magazine
  13. ↑ 13.0 13.1 Template:Cite web
  14. ↑ Template:Cite news
  15. ↑ Template:Cite news
  16. ↑ Template:Cite web
  17. ↑ Template:Cite web
  18. ↑ Template:Cite web
  19. ↑ Will Edgington's Mersenne Page Template:Webarchive
  20. ↑ Template:Cite web
  21. ↑ 21.0 21.1 There is no mentioning among the ancient Egyptians of prime numbers, and they did not have any concept for prime numbers known today. In the Rhind papyrus (1650 BC) the Egyptian fraction expansions have fairly different forms for primes and composites, so it may be argued that they knew about prime numbers. "The Egyptians used ($) in the table above for the first primes Template:Math = 3, 5, 7, or 11 (also for Template:Math = 23). Here is another intriguing observation: That the Egyptians stopped the use of ($) at 11 suggests they understood (at least some parts of) Eratosthenes's Sieve 2000 years before Eratosthenes 'discovered' it." The Rhind 2/Template:Math Table [Retrieved 2012-11-11]. In the school of Pythagoras (b. about 570 – d. about 495 BC) and the Pythagoreans, we find the first sure observations of prime numbers. Hence the first two Mersenne primes, 3 and 7, were known to and may even be said to have been discovered by them. There is no reference, though, to their special form 22 − 1 and 23 − 1 as such. The sources to the knowledge of prime numbers among the Pythagoreans are late. The Neoplatonic philosopher Iamblichus, AD c. 245–c. 325, states that the Greek Platonic philosopher Speusippus, c. 408 – 339/8 BC, wrote a book named On Pythagorean Numbers. According to Iamblichus this book was based on the works of the Pythagorean Philolaus, c. 470–c. 385 BC, who lived a century after Pythagoras, 570 – c. 495 BC. In his Theology of Arithmetic in the chapter On the Decad, Iamblichus writes: "Speusippus, the son of Plato's sister Potone, and head of the Academy before Xenocrates, compiled a polished little book from the Pythagorean writings which were particularly valued at any time, and especially from the writings of Philolaus; he entitled the book On Pythagorean Numbers. In the first half of the book, he elegantly expounds linear numbers [that is, prime numbers], polygonal numbers and all sorts of plane numbers, solid numbers and the five figures which are assigned to the elements of the universe, discussing both their individual attributes and their shared features, and their proportionality and reciprocity." Iamblichus The Theology of Arithmetic translated by Robin Waterfiled, 1988, p. 112f. [Retrieved 2012-11-11]. Iamblichus also gives us a direct quote from Speusippus' book where Speusippus among other things writes: "Secondly, it is necessary for a perfect number [the concept "perfect number" is not used here in a modern sense] to contain an equal amount of prime and incomposite numbers, and secondary and composite numbers." Iamblichus The Theology of Arithmetic translated by Robin Waterfiled, 1988, p. 113. [Retrieved 2012-11-11]. For the Greek original text, see Speusippus of Athens: A Critical Study with a Collection of the Related Texts and Commentary by Leonardo Tarán, 1981, p. 140 line 21–22 [Retrieved 2012-11-11] In his comments to Nicomachus of Gerasas's Introduction to Arithmetic, Iamblichus also mentions that Thymaridas, ca. 400 BC – ca. 350 BC, uses the term rectilinear for prime numbers, and that Theon of Smyrna, fl. AD 100, uses euthymetric and linear as alternative terms. Nicomachus of Gerasa, Introduction to Arithmetic, 1926, p. 127 [Retrieved 2012-11-11] It is unclear though when this said Thymaridas lived. "In a highly suspect passage in Iamblichus, Thymaridas is listed as a pupil of Pythagoras himself." Pythagoreanism [Retrieved 2012-11-11] Before Philolaus, c. 470–c. 385 BC, we have no proof of any knowledge of prime numbers.
  22. ↑ 22.0 22.1 Template:Cite web
  23. ↑ The Prime Pages, Mersenne Primes: History, Theorems and Lists.
  24. ↑ We find the oldest (undisputed) note of the result in Codex nr. 14908, which origins from Bibliotheca monasterii ord. S. Benedicti ad S. Emmeramum Ratisbonensis now in the archive of the Bayerische Staatsbibliothek, see "Halm, Karl / Laubmann, Georg von / Meyer, Wilhelm: Catalogus codicum latinorum Bibliothecae Regiae Monacensis, Bd.: 2,2, Monachii, 1876, p. 250". [retrieved on 2012-09-17] The Codex nr. 14908 consists of 10 different medieval works on mathematics and related subjects. The authors of most of these writings are known. Some authors consider the monk Fridericus Gerhart (Amman), 1400–1465 (Frater Fridericus Gerhart monachus ordinis sancti Benedicti astrologus professus in monasterio sancti Emmerani diocesis Ratisponensis et in ciuitate eiusdem) to be the author of the part where the prime number 8191 is mentioned. Geschichte Der Mathematik [retrieved on 2012-09-17] The second manuscript of Codex nr. 14908 has the name "Regulae et exempla arithmetica, algebraica, geometrica" and the 5th perfect number and all is factors, including 8191, are mentioned on folio no. 34 a tergo (backside of p. 34). Parts of the manuscript have been published in Archiv der Mathematik und Physik, 13 (1895), pp. 388–406 [retrieved on 2012-09-23]
  25. ↑ "A i lettori. Nel trattato de' numeri perfetti, che giàfino dell anno 1588 composi, oltrache se era passato auáti à trouarne molti auertite molte cose, se era anco amplamente dilatatala Tauola de' numeri composti , di ciascuno de' quali si vedeano per ordine li componenti, onde preposto unnum." p. 1 in Trattato de' nvumeri perfetti Di Pietro Antonio Cataldo 1603. http://fermi.imss.fi.it/rd/bdv?/bdviewer@selid=1373775#
  26. ↑ pp. 13–18 in Trattato de' nvumeri perfetti Di Pietro Antonio Cataldo 1603. http://fermi.imss.fi.it/rd/bdv?/bdviewer@selid=1373775#
  27. ↑ pp. 18–22 in Trattato de' nvumeri perfetti Di Pietro Antonio Cataldo 1603. http://fermi.imss.fi.it/rd/bdv?/bdviewer@selid=1373775#
  28. ↑ http://bibliothek.bbaw.de/bbaw/bibliothek-digital/digitalequellen/schriften/anzeige/index_html?band=03-nouv/1772&seite:int=36 Nouveaux Mémoires de l'Académie Royale des Sciences et Belles-Lettres 1772, pp. 35–36 EULER, Leonhard: Extrait d'une lettre à M. Bernoulli, concernant le Mémoire imprimé parmi ceux de 1771. p. 318 [intitulé: Recherches sur les diviseurs de quelques nombres très grands compris dans la somme de la progression géométrique 1 + 101 + 102 + 103 + ... + 10T = S]. Retrieved 2011-10-02.
  29. ↑ http://primes.utm.edu/notes/by_year.html#31 The date and year of discovery is unsure. Dates between 1752 and 1772 are possible.
  30. ↑ Template:Cite web
  31. ↑ “En novembre de l’année 1883, dans la correspondance de notre Académie se trouve une communication qui contient l’assertion que le nombre Template:Nowrap est un nombre premier. /…/ Le tome XLVIII des Mémoires Russes de l’Académie /…/ contient le compte-rendu de la séance du 20 décembre 1883, dans lequel l’objet de la communication du père Pervouchine est indiqué avec précision.” Bulletin de l'Académie Impériale des Sciences de St.-Pétersbourg, s. 3, v. 31, 1887, cols. 532–533. https://www.biodiversitylibrary.org/item/107789#page/277/mode/1up [retrieved 2012-09-17] See also Mélanges mathématiques et astronomiques tirés du Bulletin de l’Académie impériale des sciences de St.-Pétersbourg v. 6 (1881–1888), pp. 553–554. See also Mémoires de l'Académie impériale des sciences de St.-Pétersbourg: Sciences mathématiques, physiques et naturelles, vol. 48
  32. ↑ Template:Cite journal
  33. ↑ "M. E. Fauquenbergue a trouvé ses résultats depuis Février, et j’en ai reçu communication le 7 Juin; M. Powers a envoyé le 1er Juin un cablógramme à M. Bromwich [secretary of London Mathematical Society] pour Template:Math. Sur ma demande, ces deux auteurs m’ont adressé leurs remarquables résultats, et je m’empresse de les publier dans nos colonnes, avec nos felicitations." p. 103, André Gérardin, Nombres de Mersenne pp. 85, 103–108 in Sphinx-Œdipe. [Journal mensuel de la curiosité, de concours & de mathématiques.] v. 9, No. 1, 1914.
  34. ↑ "Power's cable announcing this same result was sent to the London Math. So. on 1 June 1914." Mersenne's Numbers, Scripta Mathematica, v. 3, 1935, pp. 112–119 http://primes.utm.edu/mersenne/LukeMirror/lit/lit_008s.htm [retrieved 2012-10-13]
  35. ↑ http://plms.oxfordjournals.org/content/s2-13/1/1.1.full.pdf Proceedings / London Mathematical Society (1914) s2–13 (1): 1. Result presented at a meeting with London Mathematical Society on June 11, 1914. Retrieved 2011-10-02.
  36. ↑ The Prime Pages, Template:Math: Fauquembergue or Powers?.
  37. ↑ http://visualiseur.bnf.fr/CadresFenetre?O=NUMM-3039&I=166&M=chemindefer Presented at a meeting with Académie des sciences (France) on January 10, 1876. Retrieved 2011-10-02.
  38. ↑ 38.0 38.1 "Using the standard Lucas test for Mersenne primes as programmed by R. M. Robinson, the SWAC has discovered the primes 2521 − 1 and 2607 − 1 on January 30, 1952." D. H. Lehmer, Recent Discoveries of Large Primes, Mathematics of Computation, vol. 6, No. 37 (1952), p. 61, http://www.ams.org/journals/mcom/1952-06-037/S0025-5718-52-99404-0/S0025-5718-52-99404-0.pdf [Retrieved 2012-09-18]
  39. ↑ "The program described in Note 131 (c) has produced the 15th Mersenne prime 21279 − 1 on June 25. The SWAC tests this number in 13 minutes and 25 seconds." D. H. Lehmer, A New Mersenne Prime, Mathematics of Computation, vol. 6, No. 39 (1952), p. 205, http://www.ams.org/journals/mcom/1952-06-039/S0025-5718-52-99387-3/S0025-5718-52-99387-3.pdf [Retrieved 2012-09-18]
  40. ↑ 40.0 40.1 "Two more Mersenne primes, 22203 − 1 and 22281 − 1, were discovered by the SWAC on October 7 and 9, 1952." D. H. Lehmer, Two New Mersenne Primes, Mathematics of Computation, vol. 7, No. 41 (1952), p. 72, http://www.ams.org/journals/mcom/1953-07-041/S0025-5718-53-99371-5/S0025-5718-53-99371-5.pdf [Retrieved 2012-09-18]
  41. ↑ "On September 8, 1957, the Swedish electronic computer BESK established that the Mersenne number Template:Nowrap is a prime." Hans Riesel, A New Mersenne Prime, Mathematics of Computation, vol. 12 (1958), p. 60, http://www.ams.org/journals/mcom/1958-12-061/S0025-5718-1958-0099752-6/S0025-5718-1958-0099752-6.pdf [Retrieved 2012-09-18]
  42. ↑ 42.0 42.1 A. Hurwitz and J. L. Selfridge, Fermat numbers and perfect numbers, Notices of the American Mathematical Society, v. 8, 1961, p. 601, abstract 587-104.
  43. ↑ 43.0 43.1 "If Template:Math is prime, Template:Math is called a Mersenne number. The primes Template:Math and Template:Math were discovered by coding the Lucas-Lehmer test for the IBM 7090." Alexander Hurwitz, New Mersenne Primes, Mathematics of Computation, vol. 16, No. 78 (1962), pp. 249–251, http://www.ams.org/journals/mcom/1962-16-078/S0025-5718-1962-0146162-X/S0025-5718-1962-0146162-X.pdf [Retrieved 2012-09-18]
  44. ↑ 44.0 44.1 44.2 "The primes Template:Math, Template:Math, and Template:Math which are now the largest known primes, were discovered by Illiac II at the Digital Computer Laboratory of the University of Illinois." Donald B. Gillies, Three New Mersenne Primes and a Statistical Theory, Mathematics of Computation, vol. 18, No. 85 (1964), pp. 93–97, http://www.ams.org/journals/mcom/1964-18-085/S0025-5718-1964-0159774-6/S0025-5718-1964-0159774-6.pdf [Retrieved 2012-09-18]
  45. ↑ "On the evening of March 4, 1971, a zero Lucas-Lehmer residue for Template:Math was found. Hence, Template:Math is the 24th Mersenne prime." Bryant Tuckerman, The 24th Mersenne Prime, Proceedings of the National Academy of Sciences of the United States of America, vol. 68:10 (1971), pp. 2319–2320, http://www.pnas.org/content/68/10/2319.full.pdf [Retrieved 2012-09-18]
  46. ↑ "On October 30, 1978 at 9:40 pm, we found Template:Math to be prime. The CPU time required for this test was 7:40:20. Tuckerman and Lehmer later provided confirmation of this result." Curt Noll and Laura Nickel, The 25th and 26th Mersenne Primes, Mathematics of Computation, vol. 35, No. 152 (1980), pp. 1387–1390, http://www.ams.org/journals/mcom/1980-35-152/S0025-5718-1980-0583517-4/S0025-5718-1980-0583517-4.pdf [Retrieved 2012-09-18]
  47. ↑ "Of the 125 remaining Template:Math only Template:Math was found to be prime. The test was completed on February 9, 1979 at 4:06 after 8:39:37 of CPU time. Lehmer and McGrogan later confirmed the result." Curt Noll and Laura Nickel, The 25th and 26th Mersenne Primes, Mathematics of Computation, vol. 35, No. 152 (1980), pp. 1387–1390, http://www.ams.org/journals/mcom/1980-35-152/S0025-5718-1980-0583517-4/S0025-5718-1980-0583517-4.pdf [Retrieved 2012-09-18]
  48. ↑ David Slowinski, "Searching for the 27th Mersenne Prime", Journal of Recreational Mathematics, v. 11(4), 1978–79, pp. 258–261, MR 80g #10013
  49. ↑ "The 27th Mersenne prime. It has 13395 digits and equals 244497 – 1. [...] Its primeness was determined on April 8, 1979 using the Lucas–Lehmer test. The test was programmed on a CRAY-1 computer by David Slowinski & Harry Nelson." (p. 15) "The result was that after applying the Lucas–Lehmer test to about a thousand numbers, the code determined, on Sunday, April 8th, that 244497 − 1 is, in fact, the 27th Mersenne prime." (p. 17), David Slowinski, "Searching for the 27th Mersenne Prime", Cray Channels, vol. 4, no. 1, (1982), pp. 15–17.
  50. ↑ "An FFT containing 8192 complex elements, which was the minimum size required to test M110503, ran approximately 11 minutes on the SX-2. The discovery of Template:Math (January 29, 1988) has been confirmed." W. N. Colquitt and L. Welsh, Jr., A New Mersenne Prime, Mathematics of Computation, vol. 56, No. 194 (April 1991), pp. 867–870, http://www.ams.org/journals/mcom/1991-56-194/S0025-5718-1991-1068823-9/S0025-5718-1991-1068823-9.pdf [Retrieved 2012-09-18]
  51. ↑ "This week, two computer experts found the 31st Mersenne prime. But to their surprise, the newly discovered prime number falls between two previously known Mersenne primes. It occurs when Template:Math, making it the third-largest Mersenne prime known." I. Peterson, Priming for a lucky strike Science News; 2/6/88, Vol. 133 Issue 6, pp. 85–85. http://ehis.ebscohost.com/ehost/detail?vid=3&hid=23&sid=9a9d7493-ffed-410b-9b59-b86c63a93bc4%40sessionmgr10&bdata=JnNpdGU9ZWhvc3QtbGl2ZQ%3d%3d#db=afh&AN=8824187 [Retrieved 2012-09-18]
  52. ↑ Template:Cite web
  53. ↑ "Slowinski, a software engineer for Cray Research Inc. in Chippewa Falls, discovered the number at 11:36 a.m. Monday. [that is, 1983 September 19]" Jim Higgins, "Elusive numeral's number is up" and "Scientist finds big number" in The Milwaukee Sentinel – Sep 24, 1983, p. 1, p. 11 [retrieved 2012-10-23]
  54. ↑ "The number is the 30th known example of a Mersenne prime, a number divisible only by 1 and itself and written in the form Template:Math, where the exponent Template:Math is also a prime number. For instance, 127 is a Mersenne number for which the exponent is 7. The record prime number's exponent is 216,091." I. Peterson, Prime time for supercomputers Science News; 9/28/85, Vol. 128 Issue 13, p. 199. http://ehis.ebscohost.com/ehost/detail?vid=4&hid=22&sid=c11090a2-4670-469f-8f75-947b593a56a0%40sessionmgr10&bdata=JnNpdGU9ZWhvc3QtbGl2ZQ%3d%3d#db=afh&AN=8840537 [Retrieved 2012-09-18]
  55. ↑ "Slowinski's program also found the 28th in 1982, the 29th in 1983, and the 30th [known at that time] this past Labor Day weekend. [that is, August 31-September 1, 1985]" Rad Sallee, "`Supercomputer'/Chevron calculating device finds a bigger prime number" Houston Chronicle, Friday 09/20/1985, Section 1, Page 26, 4 Star Edition [retrieved 2012-10-23]
  56. ↑ The Prime Pages, The finding of the 32nd Mersenne.
  57. ↑ Chris Caldwell, The Largest Known Primes.
  58. ↑ Crays press release
  59. ↑ Template:Cite web
  60. ↑ Silicon Graphics' press release https://web.archive.org/web/19970606011821/http://www.sgi.com/Headlines/1996/September/prime.html [Retrieved 2012-09-20]
  61. ↑ The Prime Pages, A Prime of Record Size! 21257787 – 1.
  62. ↑ GIMPS Discovers 35th Mersenne Prime.
  63. ↑ GIMPS Discovers 36th Known Mersenne Prime.
  64. ↑ GIMPS Discovers 37th Known Mersenne Prime.
  65. ↑ GIMPS Finds First Million-Digit Prime, Stakes Claim to $50,000 EFF Award.
  66. ↑ GIMPS, Researchers Discover Largest Multi-Million-Digit Prime Using Entropia Distributed Computing Grid.
  67. ↑ GIMPS, Mersenne Project Discovers Largest Known Prime Number on World-Wide Volunteer Computer Grid.
  68. ↑ GIMPS, Mersenne.org Project Discovers New Largest Known Prime Number, 224,036,583 – 1.
  69. ↑ GIMPS, Mersenne.org Project Discovers New Largest Known Prime Number, 225,964,951 – 1.
  70. ↑ GIMPS, Mersenne.org Project Discovers New Largest Known Prime Number, 230,402,457 – 1.
  71. ↑ GIMPS, Mersenne.org Project Discovers Largest Known Prime Number, 232,582,657 – 1.
  72. ↑ 72.0 72.1 Titanic Primes Raced to Win $100,000 Research Award. Retrieved on 2008-09-16.
  73. ↑ "On April 12th [2009], the 47th known Mersenne prime, 242,643,801 – 1, a 12,837,064 digit number was found by Odd Magnar Strindmo from Melhus, Norway! This prime is the second largest known prime number, a "mere" 141,125 digits smaller than the Mersenne prime found last August.", The List of Largest Known Primes Home Page, http://primes.utm.edu/primes/page.php?id=88847 [retrieved 2012-09-18]
  74. ↑ Template:Cite web
  75. ↑ Template:Cite web
  76. ↑ Template:Cite web
  77. ↑ Template:Cite web
  78. ↑ GIMPS Milestones Report. Retrieved 2019-05-17
  79. ↑ Caldwell, "The Largest Known Prime by Year: A Brief History" from the Prime Pages website, University of Tennessee at Martin.
  80. ↑ Thorsten Kleinjung, Joppe Bos, Arjen Lenstra "Mersenne Factorization Factory" http://eprint.iacr.org/2014/653.pdf
  81. ↑ Template:Cite web
  82. ↑ Template:Cite web
  83. ↑ Template:Cite book
  84. ↑ Template:Cite web
  85. ↑ Template:Cite web
  86. ↑ Template:Cite web
  87. ↑ Template:Cite web
  88. ↑ Template:Cite book
  89. ↑ Chris Caldwell: The Prime Glossary: Gaussian Mersenne (part of the Prime Pages)
  90. ↑ Template:Cite paper
  91. ↑ Template:Math and Template:Math for Template:Math = 2 to 50
  92. ↑ Template:Math for Template:Math = 2 to 160
  93. ↑ Template:Math for Template:Math = 2 to 160
  94. ↑ Template:Math for Template:Math = 1 to 160
  95. ↑ Template:Math for Template:Math = 1 to 40
  96. ↑ Template:Math for odd Template:Math = 1 to 107
  97. ↑ Template:Math for Template:Math = 2 to 200
  98. ↑ PRP records, search for (a^n-b^n)/c, that is, Template:Math
  99. ↑ PRP records, search for (a^n+b^n)/c, that is, Template:Math
  100. ↑ Template:Cite web
Retrieved from "https://en.beta.math.wmflabs.org/index.php?title=Mersenne_prime&oldid=110"