Centered hexagonal number

Template:Refimprove A centered hexagonal number, or hex number, is a centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice. Centered hexagonal numbers have practical applications in materials logistics management.

Description

Dissection of hexagonal number into six triangles with a remainder of one. The triangles can be re-assembled pairwise to give three parallelograms of Template:Math dots.

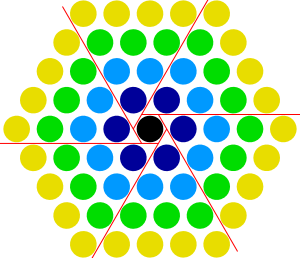
A centered hexagonal number is a centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice.

1		7		19		37
+1		+6		+12		+18

The Template:Mvarth centered hexagonal number is given by the formula

$n^{3}-(n-1)^{3}=3n(n-1)+1.\,$

Expressing the formula as

$1+6\left({1 \over 2}n(n-1)\right)$

shows that the centered hexagonal number for Template:Mvar is 1 more than 6 times the Template:Mathth triangular number.

The first few centered hexagonal numbers are Template:OEIS:

1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919.

Properties

In base 10 one can notice that the hexagonal numbers' rightmost (least significant) digits follow the pattern 1–7–9–7–1.

The sum of the first Template:Mvar centered hexagonal numbers is [[cube (algebra)|Template:Math]]. That is, centered hexagonal pyramidal numbers and cubes are the same numbers, but they represent different shapes. Viewed from the opposite perspective, centered hexagonal numbers are differences of two consecutive cubes, so that the centered hexagonal numbers are the gnomon of the cubes. (This can be seen geometrically from the diagram.) In particular, prime centered hexagonal numbers are cuban primes.

The difference between Template:Math and the Template:Mvarth centered hexagonal number is a number of the form Template:Math, while the difference between Template:Math and the Template:Mvarth centered hexagonal number is a pronic number.

Applications

Centered hexagonal numbers have practical applications in materials logistics management, for example, in packing round items into larger round containers, such as Vienna sausages into round cans, or combining individual wire strands into a cable.

Testing / finding the root

The root Template:Mvar of a centered hexagonal number Template:Mvar can be calculated using the following formula:

$n={{3+{\sqrt {12x-3}}} \over 6}$

See also

• Hexagonal number
• Magic hexagon
• Star number